OS：Windows10(64ビット)

言語：Python 3.7.6

機械学習とはAIの1つの要素技術です。

機械学習について理解するのに必要なことは3つあり、

以下のようになります。

・データからルールやパターンを発見する方法である

・識別と予測が主な使用目的である

・分析の精度は100%ではないが、従来の手法より精度をあげられる可能性は高い

Pythonは機械学習で最も使われているプログラミング言語のことです。

IBMの調査によると、「機械学習における最も人気なプログラミング言語」という項目でPythonは2016年にJavaを超えて1位になるほど機械学習には欠かせないプログラミング言語となっています。Pythonがプログラミング言語として利用されるのには以下の4つの理由が挙げられます。

・シンプルさ

・できることの多さ

・使い勝手の良さ

・豊富なライブラリやフレームワーク

Pythonは数学をあまり知らない初等教育の子どもでも取り組めるほどシンプルさがあります。また、Pythonを使えば「Google」や「Facebook」などの

webサービスから機械学習・ディープラーニングまで多くのことができます。

基礎計算を高速で行える「Numpy」や機械学習のプログラミングを楽にさせてくれる「Scikit-learn」というライブラリなど、Pythonを支えるフレームワークやライブラリーが非常に充実しており、使い勝手が良いのも多くの人に利用される要因です。

Chainer (チェイナー) は、ニューラルネットワークの計算および学習を行うためのオープンソースのソフトウェアライブラリである。バックプロパゲーション(※誤差逆伝播法)に必要なデータ構造をプログラムの実行時に動的に生成する特徴があり複雑なニューラルネットワークの構築を必要とするディープラーニング（深層学習)で用いられる。Python 2.x系および3.x系から利用でき、GPUによる演算をサポートしている。

※誤差逆伝播法：機械学習 において、 ニューラルネットワーク を学習させる際に用いられる アルゴリズム である。

コンピューターによる情報処理方法の一つ。ニューロンに相当する基本素子を結んでいる配列網。人間の脳神経系を解明し，それを技術の力で実現しようとする試みで，各素子の重みベクトルを変化させることにより，人間と同様に学習することができる。

最もシンプルなニューラルネットワーク

中間層が存在するニューラルネットワーク

手書き文字のサンプル画像データを可視化

import numpy as np

import matplotlib.pyplot as plt

import chainer.optimizers as Opt

import chainer.functions as F

import chainer.links as L

from chainer import Variable,Chain,config

import chainer.datasets as ds

import chainer.dataset.convert as con

#ニューラルネットワークのモデルを定義

def model(x):

    # 線形変換１を実行

    h = NN.l1(x)

    # 非線形変換を実行

    h = F.relu(h)

    # バッチ規格化を実行(データの整理整頓)

    h = NN.bnorm1(h)

    # 線形変換２を実行

    y = NN.l2(h)

    return y

# グラフを表示

def plot_result2(result1,result2,title,xlabel,ylabel,

                             ymin=0.0,ymax=1.0):

    Tall = len(result1)

    plt.figure(figsize=(8,6))

    plt.plot(range(Tall), result1)

    plt.plot(range(Tall), result2)

    plt.title(title)

    plt.xlabel(xlabel)

    plt.ylabel(ylabel)

    plt.xlim([0,Tall])

    plt.ylim([ymin,ymax])

    plt.show()

# 学習と成果の結果を取得

def learning_classification(model,optNN,data,result,T=10):

    for time in range(T):

        # トレーニングモードON

        config.train = True

        # 初期化

        optNN.target.zerograds()

        # トレーニングを実行し結果を取得

        ytrain = model(data[0])

        # 現状の結果と正解がどれだけ近いのかを示す誤差関数の計算を実施

        loss_train = F.softmax_cross_entropy(ytrain,data[2])

        # 現状の成績をチェックする

        acc_train = F.accuracy(ytrain,data[2])

        # 誤差関数の計算過程を振り返って誤差逆伝搬法を実行

        loss_train.backward()

        # ニューラルネットワークの最適化実行

        optNN.update()

        # トレーニングモードOFF（テストモード）

        config.train = False

        # テストを実行し結果を取得

        ytest = model(data[1])

        # 現状の結果と正解がどれだけ近いのかを示す誤差関数の計算を実施

        loss_test = F.softmax_cross_entropy(ytest,data[3])

        # 現状の成績をチェックする

        acc_test = F.accuracy(ytest,data[3])

        # 誤差関数の計算結果を保存(トレーニングモード)

        result[0].append(loss_train.data)

        # 誤差関数の計算結果を保存(テストモード)

        result[1].append(loss_test.data)

        # 成績の計算結果を保存(トレーニングモード)

        result[2].append(acc_train.data)

        # 成績の計算結果を保存(テストモード)

        result[3].append(acc_test.data)

        # 学習回数を表示

        print(time)

# 手書き画像データを取得（訓練データとテストデータ）

train,test = ds.get_mnist()

# 訓練データを訓練用画像データと訓練画像判定結果データに分ける

xtrain,ttrain = con.concat_examples(train)

# テストデータをテスト用画像データとテスト画像判定結果データに分ける

xtest,ttest = con.concat_examples(test)

# 訓練用画像データの形を確認（Dtrain：画像データ個数。N：１つの画像データのデータ数）

Dtrain,N = xtrain.shape

# Dtrain=60000、N=784

print(Dtrain,N)

# テスト用画像データの形を確認（xtest：画像データ個数。N：１つの画像データのデータ数）

Dtest,Nt = xtest.shape

# Dtrain=10000、N=784

print(Dtest,Nt)

# 訓練用画像データの一部(3画像)を確認

plt.imshow(xtrain[0,:].reshape(28,28))

plt.show()

plt.imshow(xtrain[1,:].reshape(28,28))

plt.show()

plt.imshow(xtrain[2,:].reshape(28,28))

plt.show()

# 訓練画像判定結果データの最大値＋１を出力個数とする(数値は0から9の10種類)。

C = ttrain.max()+1

# ニューラルネットワークを定義する

NN = Chain(

    # N入力、400出力の線形変換１

    l1=L.Linear(N,400),

    # 400入力、C出力の線形変換２

    l2=L.Linear(400,C),

    # ニューラルネットワークのバッチ規格化(途中の結果の整理整頓を行い学習を安定化させる役目をもつ)

    bnorm1 =  L.BatchRenormalization(400))

'''

線形変換とはN個の数値にそれぞれ重みを掛け足し合わせてC個の数値へと変換する。

そうした「数値の組み合わせ」を考えるのがニューラルネットワークで行われる。

'''

# ニューラルネットワークの最適化手法の設定（「MomentumSGD」という最適化手法を指定）

optNN = Opt.MomentumSGD()

optNN.setup(NN)

# データと学習の記録を残す場所を定義

train_loss = []

train_acc = []

test_loss = []

test_acc = []

# データと結果を準備

data = [xtrain,xtest,ttrain,ttest]

result = [train_loss,test_loss,train_acc,test_acc]

# 学習用関数を呼び出す

learning_classification(model,optNN,data,result)

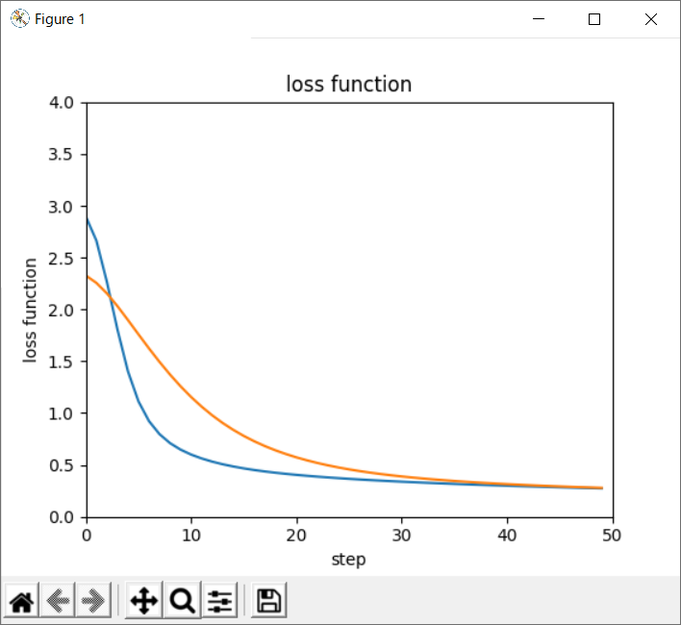
# 結果をグラフ表示(訓練結果：青線、テスト結果：オレンジ線)

plot_result2(result[0],result[1],"loss function","step","loss function",0.0,4.0)

plot_result2(result[2],result[3],"accuracy","step","accuracy")

手書き文字の画像判定結果のデータを表示させてみると、

７の画像判定結果

variable([

[ 0.52532893 -1.5429686  -1.2219387   0.7525703  -1.4716352

  -0.985907   -2.6790137   9.64561    -4.068186    3.3250828 ]

])

２の画像判定結果

variable([

[ 2.0151818  -0.39250198  7.2630014   2.2690983  -5.5832

  1.4664513   4.3449802  -7.575552    1.8654045  -7.3400116 ]

])

１の画像判定結果

variable([

[-2.2883766   5.346202    0.520786   -0.7446091   0.04422885

 -0.81961423  0.3979009   1.293481   -0.8722219  -1.3619449 ]

])

０の画像判定結果

variable([

[ 8.766278   -2.891544   -1.0571241  -3.0388563  -3.3963797

  0.13687362  1.9502935   0.15858142 -3.5175889  -1.1633263 ]

])

４の画像判定結果

variable([

[-1.501171   -1.187334   -0.7797193  -3.4468813   5.103101

 -1.1305952  -0.08878505  2.0099173  -1.537114    2.4908376 ]

])

今回、50回学習をさせた。１回あたりの学習で約１秒ほどかかっていたので50秒ということになる。複雑なニューラルネットワークであればもっと処理時間を要すると思われる。ChainerはGPUがサポートされているので、GPUを学習の計算処理に使用した場合どれくらいスピードアップできるのか次回検証してみたいと思います。